Search

50. Pow(x, n)

Implement pow(x, n), which calculates x raised to the power n (i.e., xn).
Example 1:
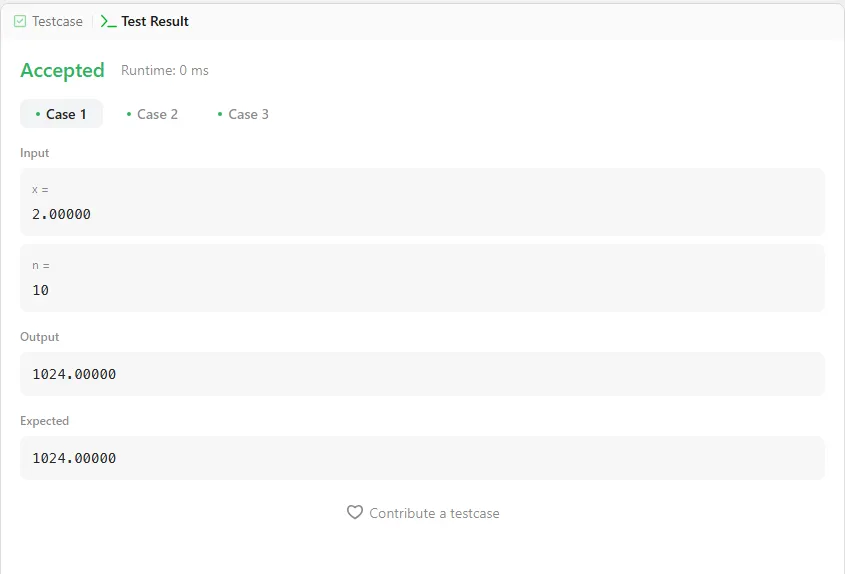
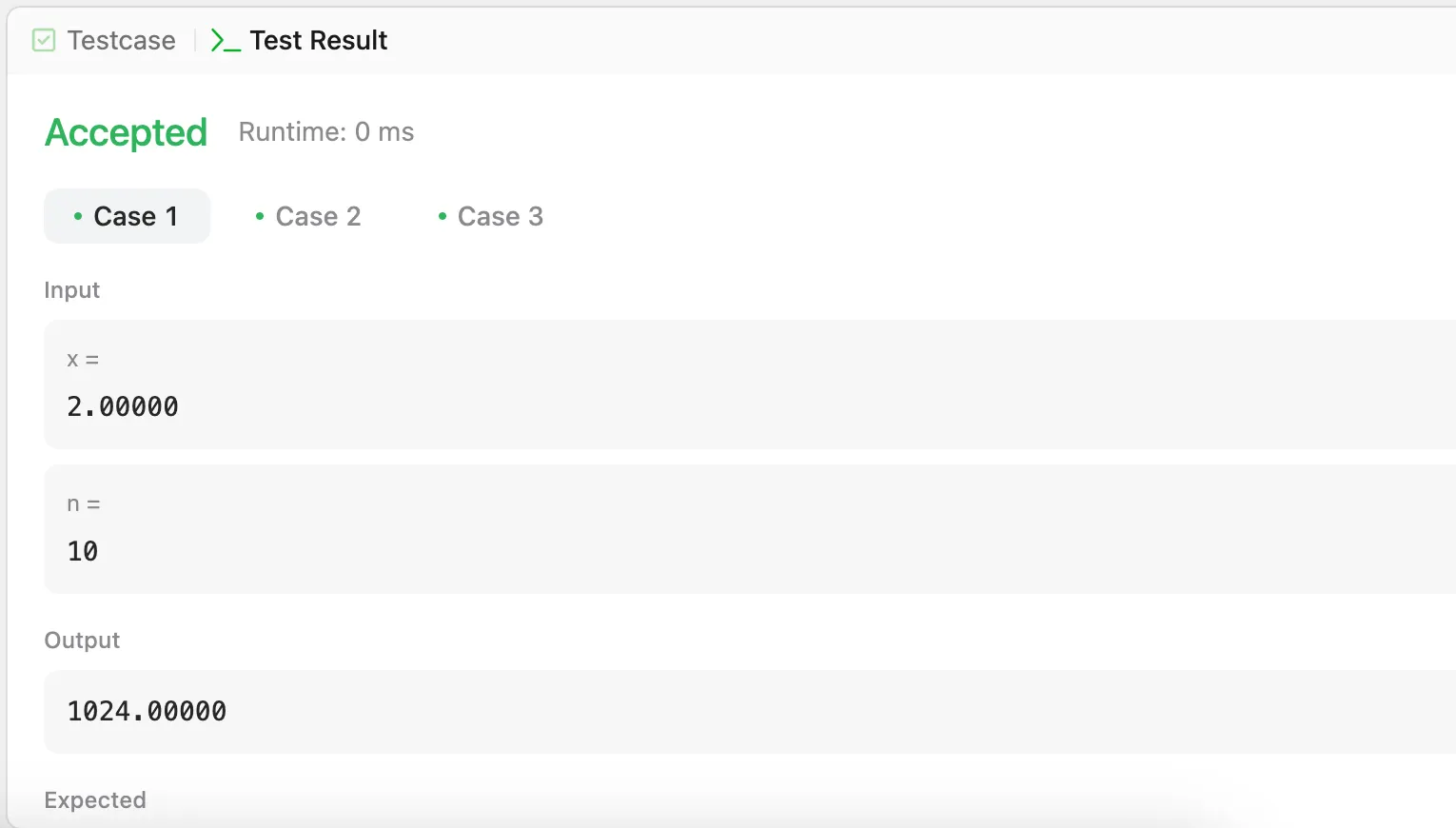
Input: x = 2.00000, n = 10 Output: 1024.00000
Plain Text
복사
Example 2:
Input: x = 2.10000, n = 3 Output: 9.26100
Plain Text
복사
Example 3:
Input: x = 2.00000, n = -2 Output: 0.25000 Explanation: 2-2 = 1/22 = 1/4 = 0.25
Plain Text
복사
Constraints:
•
100.0 < x < 100.0
•
−231-2^{31} < n < 2312^{31}
•
n is an integer.
•
Either x is not zero or n > 0.
•
104 <= xn <= 104
link to the problem
This is my first time attempting a medium-level problem after only solving easy ones. Let’s take a look at the problem. At first glance, it seemed like I could simply compute xnx^n, but looking at Example 3 and the problem’s constraints, I realized that nn could also be negative. In that case, simply doing xnx^n would produce the wrong answer.
Therefore, I need to design the program to account for the reciprocal of the power. Now, let’s write the code…
30 minutes later…
class Solution: def myPow(self, x: float, n: int) -> float: result = 0 if n < 0: # First, convert it to a positive number, calculate the power, and then divide 1 by the result. # In Python, you can reverse the sign by adding a minus sign. n = -n result = 1 / (x ** n) else: result = x ** n return float(result)
Python
복사
If n is negative, first convert the exponent to a positive number, compute the power, and then take the reciprocal of the result. For example, if x is 2 and n is -2, first calculate 222^2 to get 4, then divide 1 by 4 to obtain 0.25. If n is positive, simply compute xnx^n, and if n is 0 while x is not 0, the result is 1. However, if x is 0 and n is negative, the result is undefined because it involves division by zero.
The test cases passed successfully, so let’s go ahead and submit the answer.
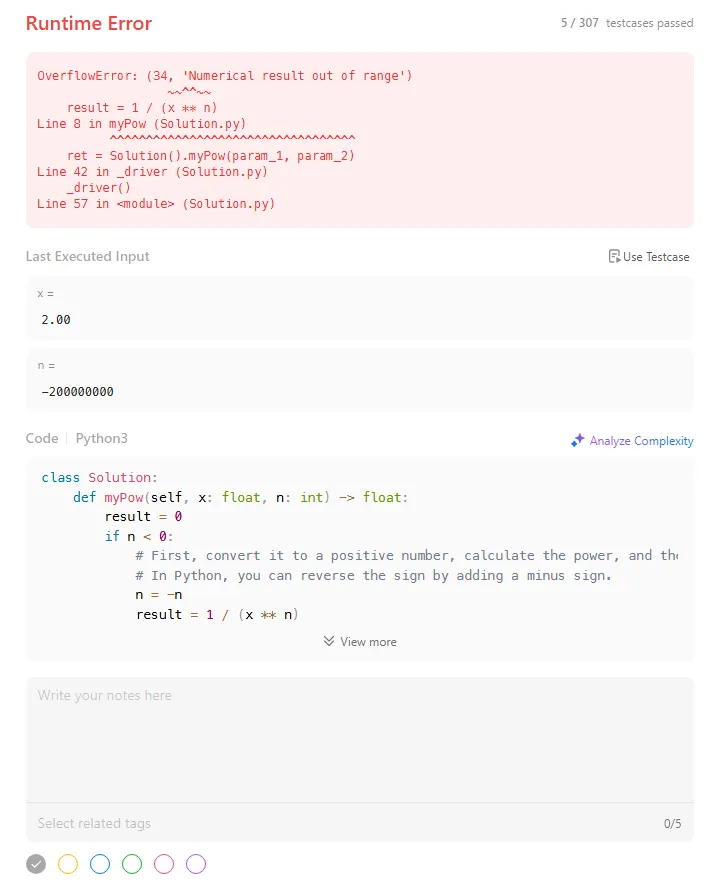
After submitting my answer, a runtime error occurred. I guess a Medium problem isn’t called Medium for nothing…
Looking at the error message, it shows an OverflowError, which happens when the result of a numerical operation exceeds the range that the data type can represent.
Reviewing the problem’s constraints, I found that n is in the range −231-2^{31} < n < 2312^{31}. In other words, 2312^{31} equals 2,147,483,648, so the range of n is −2,147,483,648 < n < 2,147,483,648

Second try

class Solution: def myPow(self, x: float, n: int) -> float: result = 0 if n < 0: # First, convert it to a positive number, calculate the power, and then divide 1 by the result. # In Python, you can reverse the sign by adding a minus sign. n = -n result = float(1 / (x ** n)) else: result = float(x ** n) return result
Python
복사
At first, I only wrapped the return value with float at the end, but since the overflow occurred when assigning the value to result inside the if and else blocks, I wrapped it with float during the calculation instead. I’ll submit the code with this change…
The second attempt was another complete failure! What stands out here is that the error message is exactly the same as before. This means that the approach I took was likely wrong. Reading the error message again carefully, it says, “Numerical result out of range.” This error occurs when the result of a calculation exceeds the capacity of the data type to store it.
And when I read the error message again, I realized that LeetCode was actually kind enough to tell me exactly which test case caused the error… but in my usual haste, I completely overlooked it.
It seems I’ve finally pinpointed the cause. If you calculate 2−2000000002^{-200000000}, the number becomes something like 0.0000000… so small that it cannot be represented with that level of precision using a float.
(I’m once again acutely realizing why this is a Medium-level problem…)

Final try

class Solution: def myPow(self, x: float, n: int) -> float: def fast_pow(base, exp): if exp == 0: # If the exponent is 0, the result is 1 regardless of the base. return 1 half = fast_pow(base, exp // 2) # Recursively calculate by halving the exponent. if exp % 2 == 0: # If the exponent is even, square it as is. return half * half else: # If the exponent is odd, multiply by the base once more. return half * half * base if n < 0: # If the exponent is negative, return the reciprocal. return 1 / fast_pow(x, -n) else: return fast_pow(x, n)
Python
복사
I found that to solve the problem, you need to use the fast exponentiation method, which should have a time complexity of O(log n).
In other words, with each operation, the number of calculations to be performed should be reduced by half.
For example, to calculate 282^8, you would normally do 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2, right?
That means performing n operations, resulting in a time complexity of O(n).
However, 282^8 can also be expressed as 242^4 × 242^4. And 242^4 can again be expressed as 222^2 × 222^2.
다행히 테스트케이스는 무사히 통과했다. 그럼 답안 제출을 해보자