Given two binary strings a and b, return their sum as a binary string.
Example 1:
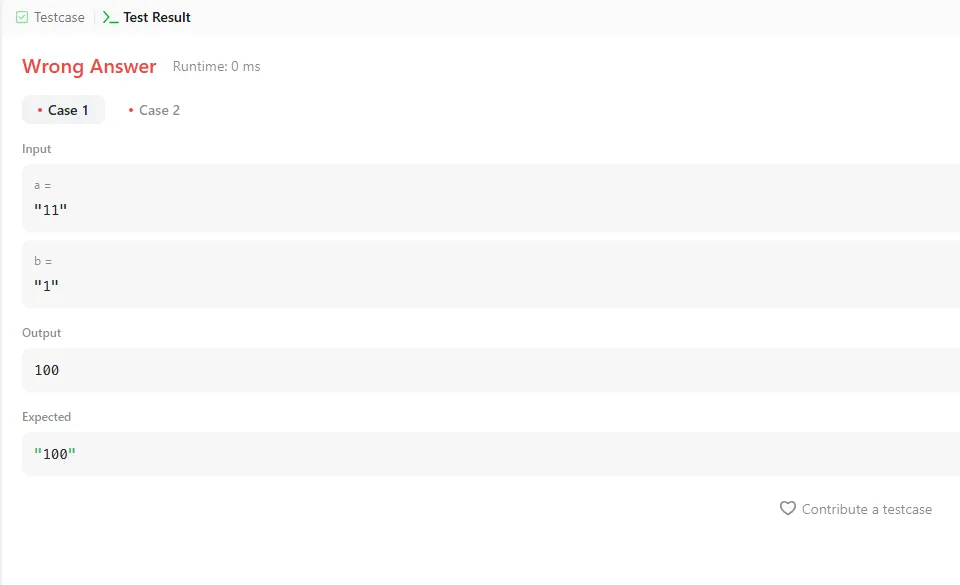
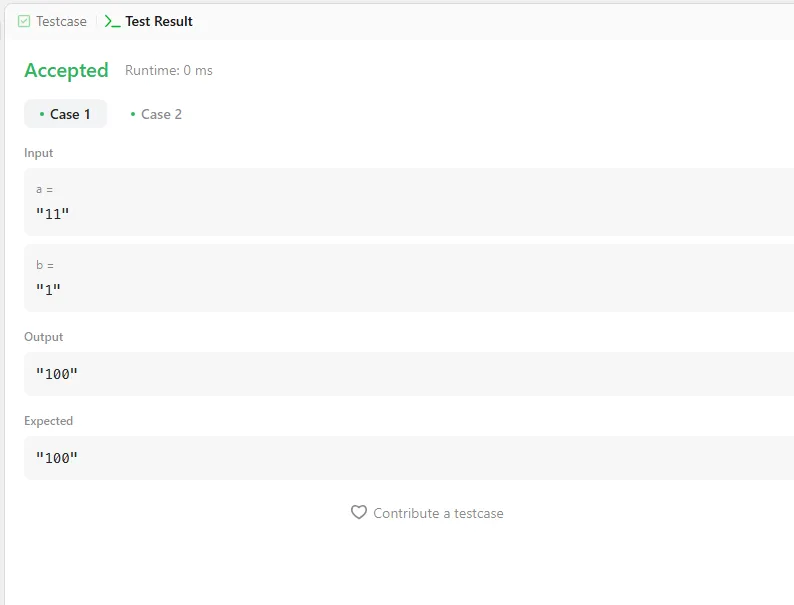
Input: a = "11", b = "1"
Output: "100"
Plain Text
복사
Example 2:
Input: a = "1010", b = "1011"
Output: "10101"
Plain Text
복사
Constraints:
•
1 <= a.length, b.length <= 104
•
a and b consist only of '0' or '1' characters.
•
Each string does not contain leading zeros except for the zero itself.
At first, when I read the problem, the idea that came to mind was to convert the two binary numbers a and b given as parameters into decimal for easier calculation, add them together, and then convert the result back into binary. Of course, this is not the most computer-efficient approach, but since this was the idea I came up with, I decided to give it a try.
class Solution:
def addBinary(self, a: str, b: str) -> str:
a = int(self.binary_to_decimal(a))
b = int(self.binary_to_decimal(b))
return int(self.decimal_to_binary(a + b))
def decimal_to_binary(self, decimal:str) -> str:
result = ''
n = int(decimal)
while n > 0:
remainder = n % 2
result = str(remainder) + result
n = n // 2
# if answer is empty, return '0' instead
return result if result else '0'
def binary_to_decimal(self, binary:str) -> str:
result = 0
i = 0
while i < len(binary):
if binary[i] == '1':
# Add the power of 2 for the corresponding digit.
"""
The reason for subtracting `-1` in `(len(binary) - i - 1)` is because the length of the string and the starting point of the index are different.
`len(binary)` represents the total number of digits, while the index `i` starts from 0. For example,
in a 4-digit binary number `1010`, the leftmost digit (index 0) actually corresponds to the 2^3 place.
However, if we calculate using `len(binary) - i`, it would result in 2^4, which is incorrect.
By subtracting 1, index 0 becomes $2^3$, index 1 becomes 2^2, index 2 becomes 2^1, and index 3 becomes 2^0, ensuring that the exponent is calculated correctly.
"""
result += 2 ** (len(binary) - i - 1)
i += 1
return str(result)
Python
복사
decimal_to_binary function converts a decimal value into its binary string representation. It first converts the input decimal string into an integer, then repeatedly divides the number by 2 until the quotient becomes 0. In each iteration, it calculates the remainder when dividing n by 2, converts it into a string, and prepends it to the result string. This ensures that the binary digits are built in the correct order instead of reversed. When the loop ends, if the result string is empty (which happens if the input value was 0), it returns '0'. Otherwise, it returns the computed binary string.
binary_to_decimal function converts a binary string into its decimal string represenation. It iterates through the binary string from left to right, and whenever the current character is ‘1’ , it adds the value of 2 exponent for that position to the result. The exponent is calculated as len(binary) - i - 1 , because the total length of the string (len(binary)) and the index i have different starting points, len(binary) counts from 1, but i starts at 0. Subtracting 1 ensures the correct exponent for each position. For example in “1010” , index 0 corresponds to , so (4 - 0 - 1) = 3. This process continues for all positions, and the final decimal value is returned as a string
When I submitted the code, it was marked incorrect because the expected value was "100", but my answer returned 100. It seems I need to add double quotes to the answer.
After modifying the code, I was fortunately able to pass the test case. Unexpectedly, there was an error in a part I hadn’t even considered.
def addBinary(self, a: str, b: str) -> str:
a = int(self.binary_to_decimal(a))
b = int(self.binary_to_decimal(b))
return int(self.decimal_to_binary(a + b))
Python
복사
In the code above, if you wrap the return value with int right before returning, it becomes a decimal number again. That’s why the earlier output of 100 wasn’t a string "100", but the decimal integer 100. So I removed the int wrapper.
The final code is as follows.
class Solution:
def addBinary(self, a: str, b: str) -> str:
a = int(self.binary_to_decimal(a))
b = int(self.binary_to_decimal(b))
return self.decimal_to_binary(a + b)
def decimal_to_binary(self, decimal:str) -> str:
result = ''
n = int(decimal)
while n > 0:
remainder = n % 2
result = str(remainder) + result
n = n // 2
# if answer is empty, return '0' instead
return result if result else "0"
def binary_to_decimal(self, binary:str) -> str:
result = 0
i = 0
while i < len(binary):
if binary[i] == '1':
# Add the power of 2 for the corresponding digit.
"""
The reason for subtracting `-1` in `(len(binary) - i - 1)` is because the length of the string and the starting point of the index are different.
`len(binary)` represents the total number of digits, while the index `i` starts from 0. For example,
in a 4-digit binary number `1010`, the leftmost digit (index 0) actually corresponds to the 2^3 place.
However, if we calculate using `len(binary) - i`, it would result in 2^4, which is incorrect.
By subtracting 1, index 0 becomes $2^3$, index 1 becomes 2^2, index 2 becomes 2^1, and index 3 becomes 2^0, ensuring that the exponent is calculated correctly.
"""
result += 2 ** (len(binary) - i - 1)
i += 1
return str(result)
Python
복사
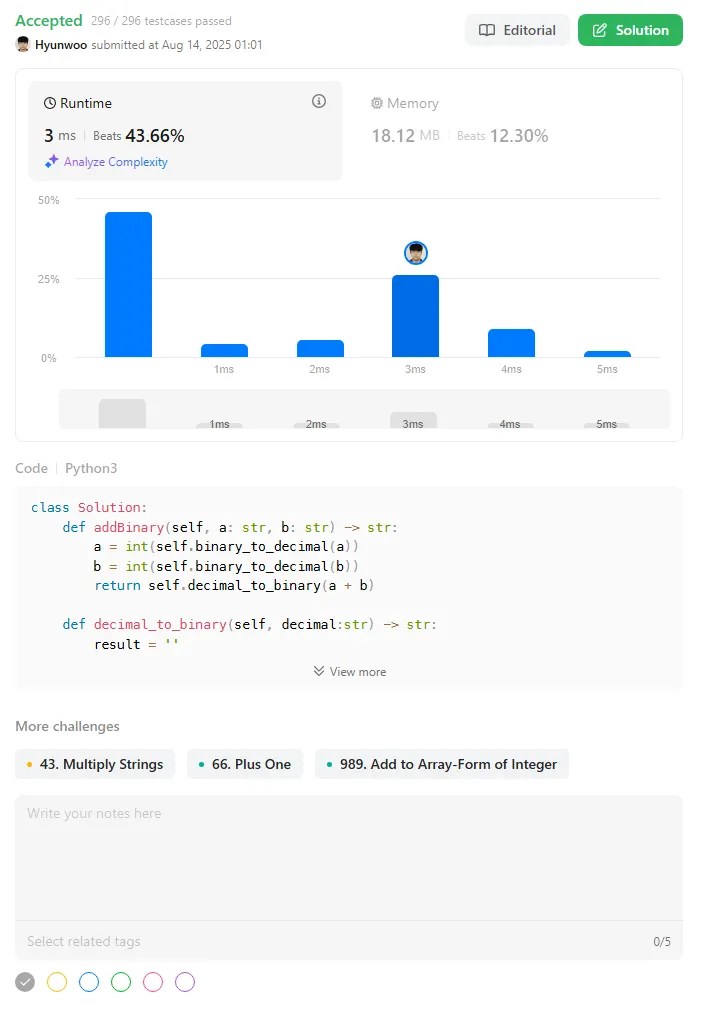
When I submitted it, it was accepted as correct.