Given a sorted array of distinct integers and a target value, return the index if the target is found. If not, return the index where it would be if it were inserted in order.
You must write an algorithm with O(log n) runtime complexity.
Example 1:
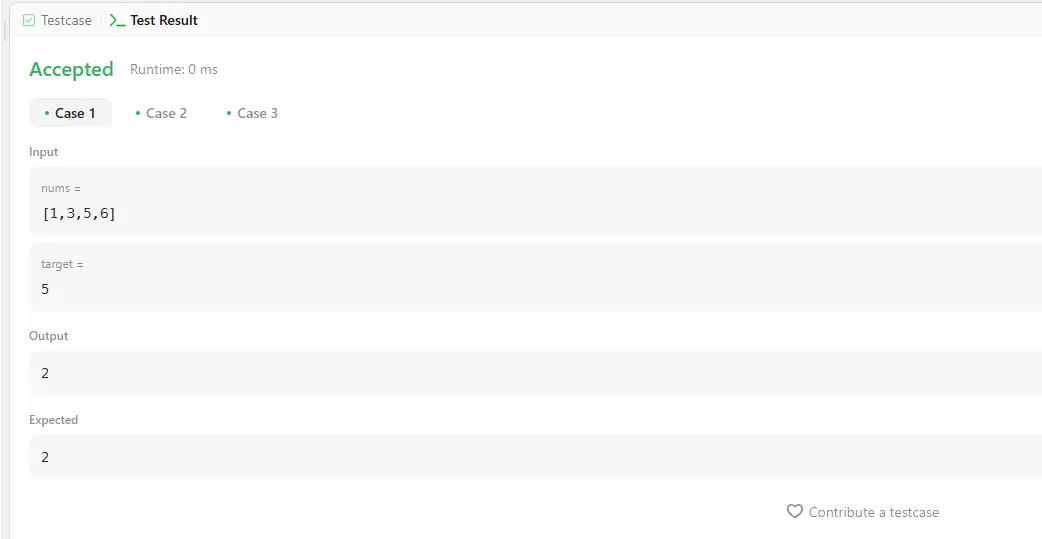
Input: nums = [1,3,5,6], target = 5
Output: 2
Plain Text
복사
Example 2:
Input: nums = [1,3,5,6], target = 2
Output: 1
Plain Text
복사
Example 3:
Input: nums = [1,3,5,6], target = 7
Output: 4
Plain Text
복사
Constraints:
•
1 <= nums.length <= 104
•
104 <= nums[i] <= 104
•
nums contains distinct values sorted in ascending order.
•
104 <= target <= 104
When I first read the problem, I thought I could simply use a loop to check if the target value exists and return its index. However, after reading the problem again, I saw that it specifically requires a time complexity of O(log n).
But using a simple loop has a time complexity of O(n)... So the requirement for O(log n) clearly suggests that the problem is meant to be solved using binary search.
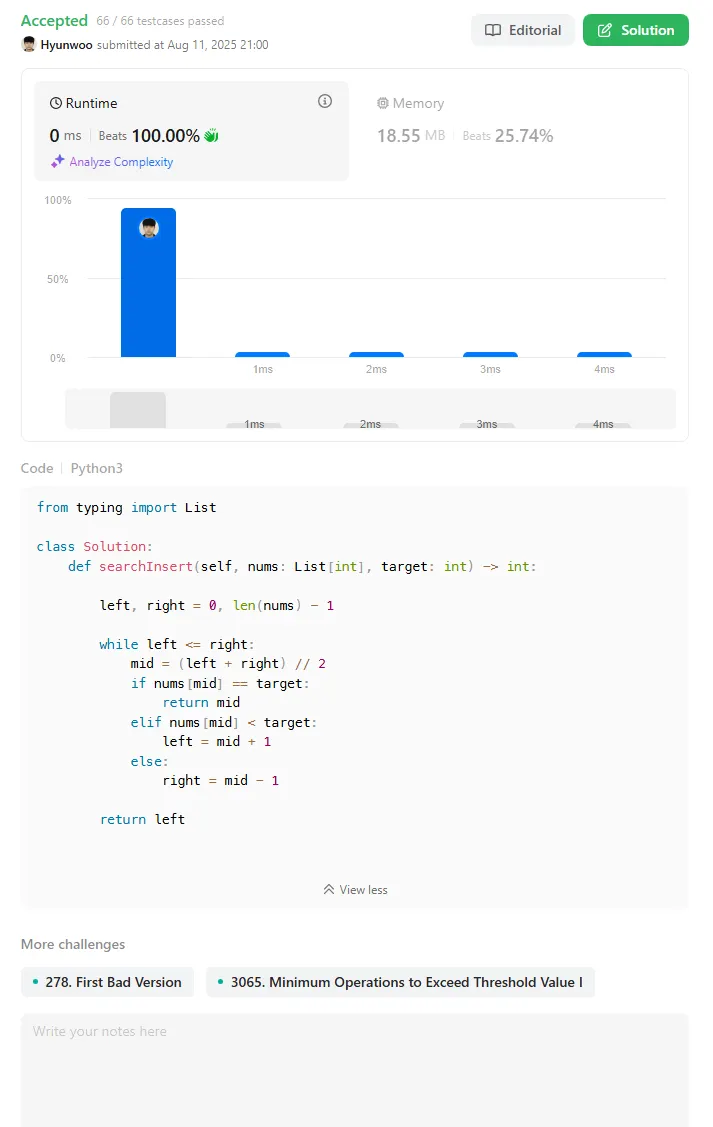
from typing import List
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1
while left <= right:
mid = (left + right) // 2
if nums[mid] == target:
return mid
elif nums[mid] < target:
left = mid + 1
else:
right = mid - 1
return left
Python
복사
This code is a binary search algorithm that either finds a given value target in a sorted list or returns the exact position where the value should be inserted while preserving the sorted order if it does not exist. The core principle of binary search is to repeatedly halve the search range until the target is found. At the start, left is set to 0 and right to len(nums) - 1, making the entire list the initial search range.
Throughout the process, the following invariants are maintained: (1) If the target exists, it must lie within the current search range [left, right]. (2) All elements to the left of left are smaller than the target, and all elements to the right of right are greater than the target. These invariants ensure that, after each comparison, one half of the range can be safely discarded.
The loop runs while left <= right, calculating the middle index as mid = (left + right) // 2 and comparing nums[mid] with the target. If the two values are equal, mid is returned immediately, ending the search. If nums[mid] < target, then mid and all elements to its left are smaller than the target, so the search range’s left boundary is updated to left = mid + 1. For example, in the list [1,2,3,4,5,6,7,8,9,10] with target = 7, the initial left = 0 and right = 9 yield mid = 4, where nums[4] = 5.
Since 5 < 7, left becomes 5, and indices 0–4 are excluded from further consideration. Conversely, if nums[mid] > target, then mid and all elements to its right are greater than the target, so the right boundary is updated to right = mid - 1. In the same list with target = 3, mid = 4 gives nums[4] = 5; since 5 > 3, right becomes 3, excluding indices 4–9.
Repeating this process progressively narrows the search range until left > right, at which point the loop terminates. Thanks to the maintained invariants, left will now indicate the earliest position where the target can be inserted while keeping the list sorted (the lower bound). Therefore, if the target exists in the array, its index is returned; if not, the insertion position is returned. Because the search range is halved in each step, the time complexity is O(log n), and since it uses only constant extra memory, the space complexity is O(1).
Given the list [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] and target 7, we should return index 6 where 7 is located. The steps are as follows.
Initial State
•
List : [1,2,3,4,5,6,7,8,9,10]
•
target = 7
•
left = 0, right = 9 (entire range)
Round 1
•
mid = (0 + 9) // 2 = 4
•
nums[mid] = 5
•
Comparison : 5 == 7 →  , 5 < 7 →
, 5 < 7 → 
•
Update left = mid + 1 = 5
•
Remaining search range : index 5–9 → [6,7,8,9,10]
Round 2
•
left = 5, right = 9
•
mid = (5 + 9) // 2 = 7
•
nums[mid] = 8
•
Comparison : 8 == 7 →  , 8 < 7 →
, 8 < 7 → 
•
Update right = mid - 1 = 6
•
Remaining search range : index 5–6 → [6,7]
Round 3
•
left = 5, right = 6
•
mid = (5 + 6) // 2 = 5
•
nums[mid] = 6
•
Comparison : 6 == 7 →  , 6 < 7 →
, 6 < 7 → 
•
Update left = mid + 1 = 6
•
Remaining search range : index 6–6 → [7]
Round 4
•
left = 6, right = 6
•
mid = (6 + 6) // 2 = 6
•
nums[mid] = 7
•
Comparison : 7 == 7 → 
•
Return result : 6 (index of the target)
•
Found the target in 4 rounds.
•
Each round halves the search range, making the process highly efficient.
•
Time complexity : O(log n).
When I ran the code, all three test cases were accepted. Now, let’s go ahead and officially submit the solution.
This time, my code luckily passed on the first try. While luck certainly played a part, I struggled quite a bit trying to implement binary search from scratch. I had to look things up on Google several times while writing the code.
The biggest takeaway from this challenge was realizing that binary search only works on sorted lists. If the data isn’t sorted, the logic of discarding half of the search range simply doesn’t make sense.
Solving this problem felt like more than just getting the correct answer. I came away with a clearer understanding of why this approach works and when it can be applied. Moving forward, I want to build the habit of checking the prerequisites before jumping straight into coding, rather than rushing to write a solution.